Research
Optimal transport meets independence testing
Optimal transport (OT) is widely studied in probability theory and has tons of applications in modern machine learning. Statistically, OT solve the problem that is, find a measurable transform map $T$ such that the distribution distance between two empirical measures $\mu_n,\nu_n$ are minimized. Usually the distance function is chosen as the p-Wasserstein distance. The transformed data $\widehat{T}(\mu_n)$ can be intuitively regarded a multivariate rank. This is super clear for one-dimensional case: the population transform map $T$ is just the CDF of $\mu$ and the transformed data is just the reference data after resorting. For multivariate case, the transformed data $\widehat{T}(\mu_n)$ does not correspond to a clear ordering of original data $\nu_n$ but can still be attractive to be viewed as rank of $\mu_n$. A figure from Nabarun’s breakthrough paper is given below.
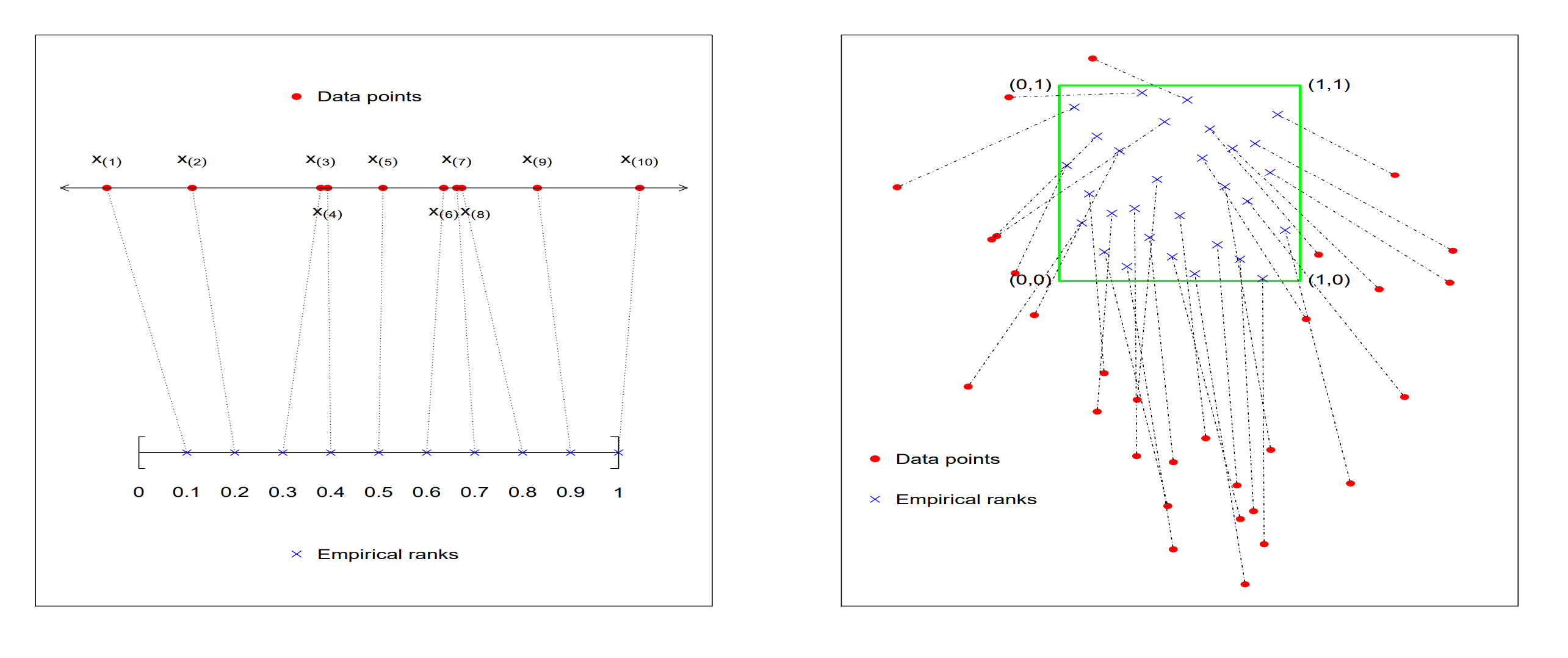
Then why is this idea appealing to nonparametric statistics community? Statisticians have searched for several decades to find a distribution-free independence test for multivariate data. There are so many proposed tests that it is too hard to even list all of their names. OT, as argued above, provides a fabulous proposal to solve such a long-standing open problem. The idea is as follows:
- Choose two reference measures that are target distribution in OT;
- Perform OT for two data matrix that need to be testing to the reference distribution;
- Plug them into any consistent test statistic, e.g. distance covariance, HSIC etc.
Done! In step 1, one can choose any reference distribution and typical choices include uniform distribution, Gaussian distribution etc. Another question is when should we reject/accept the hypothesis? In other words, finding the cutoff is important. Previously, people often apply resampling-based or permutation-based to approximate the intractable limiting distribution (Often it is infinite sum of $\chi$-squared!), which requires heavy computation. Another marvelous property for using OT-based test is, only a finite number of permutations are needed to guarantee both finite sample type-I error and power against alternative (asymptotically).
High-dimensional causal inference with presence of unobserved confounding
One of core goals of social and genetic sciences is to investigating how a treatment (e.g. peer effect, gene expression) impacts the outcome of interest (e.g. income, clinical phenotype). Often, there are, inevitably, a lot of unobserved confounding variables which affect the treatment and outcome. Ignoring them will induce spurious relationship and thus introduce bias when inferring the causal effect. Typically the treatment variable presents high-dimensionality in these applications, which pose more challenge. With the help of instrumental variable(IV), a nice two-stage estimation and inference framework is developed to tackle such problem, under which the flexible modeling methods between IV and treatment are allowed. In a mouse obesity dataset, a set of new gene expressions in liver tissue that were not discovered before, are found to influence the weight of mouse. Details are here.
Boosting the inference for intractable likelihood models using quasi-Monte Carlo method
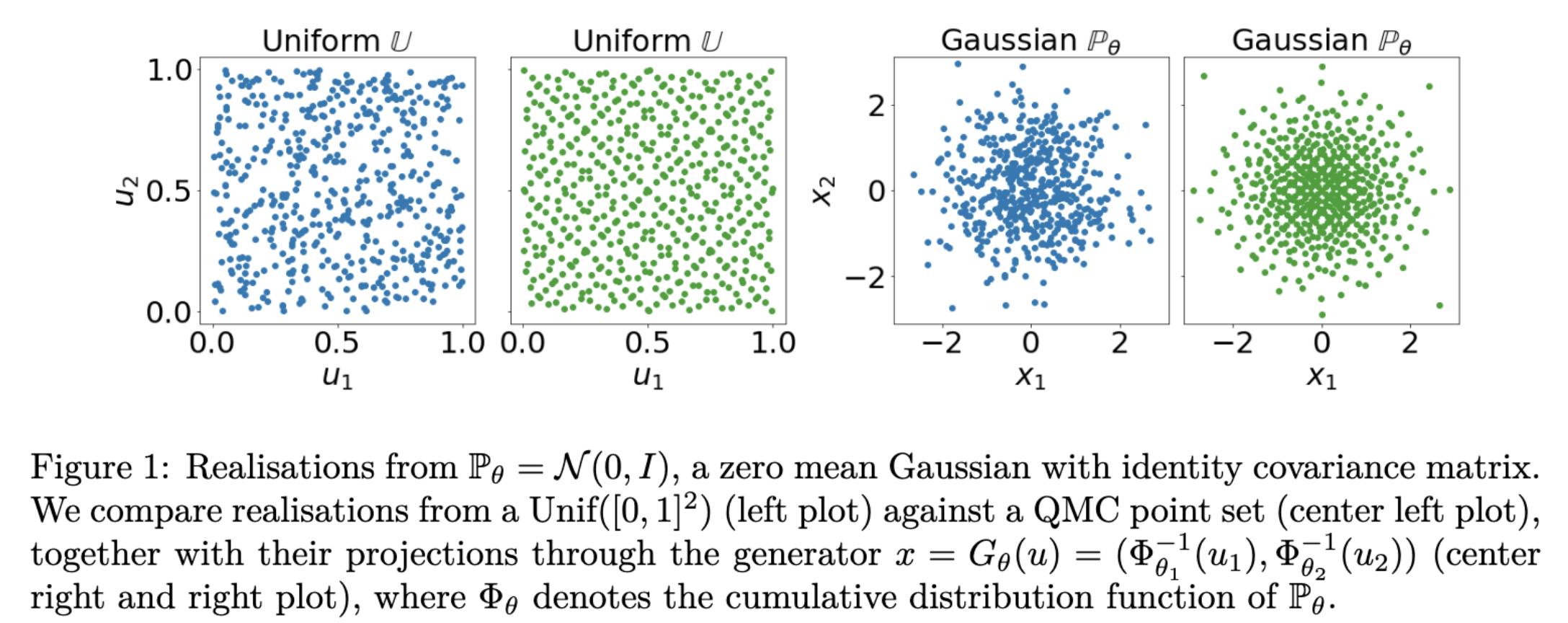
Quasi-Monte Carlo method (QMC) is an important numerical technique for approximating intractable integral using low-discrepancy sequences (also called quasi-random sequences or sub-random sequences). Compared with Monte Carlo method, an attractive feature QMC method enjoys is the approximation error can be improved to O(1/n) when the integrand is “nice” enough. A wonderful introduction for QMC method can be found in a chapter of a recent book by Art Owen. Such improvement of approximation is crucial and desired when handling the inference for intractable likelihood models, which has been commonly considered in modern machine learning and statistics applications. Typically, minimum distance estimator can be used for parameter estimation via minimizing some distance metric (many candidates inclusing integral probability metric) between the probability measure after the parametrizatioin and the empirical distribution of data. Such inferential procedure always invovles computing some intractable integrals, where QMC can be of great help and specifically, the sample complexity can be proved to decrease theoretically with QMC applied. The figure below illustrates the empirical performance on the generative neural netowrk models using different metrics inclusing maximum mean discrepancy (MMD), sliced Wassertein distance (SW), Sinkhorn divergence (S). Details are here.
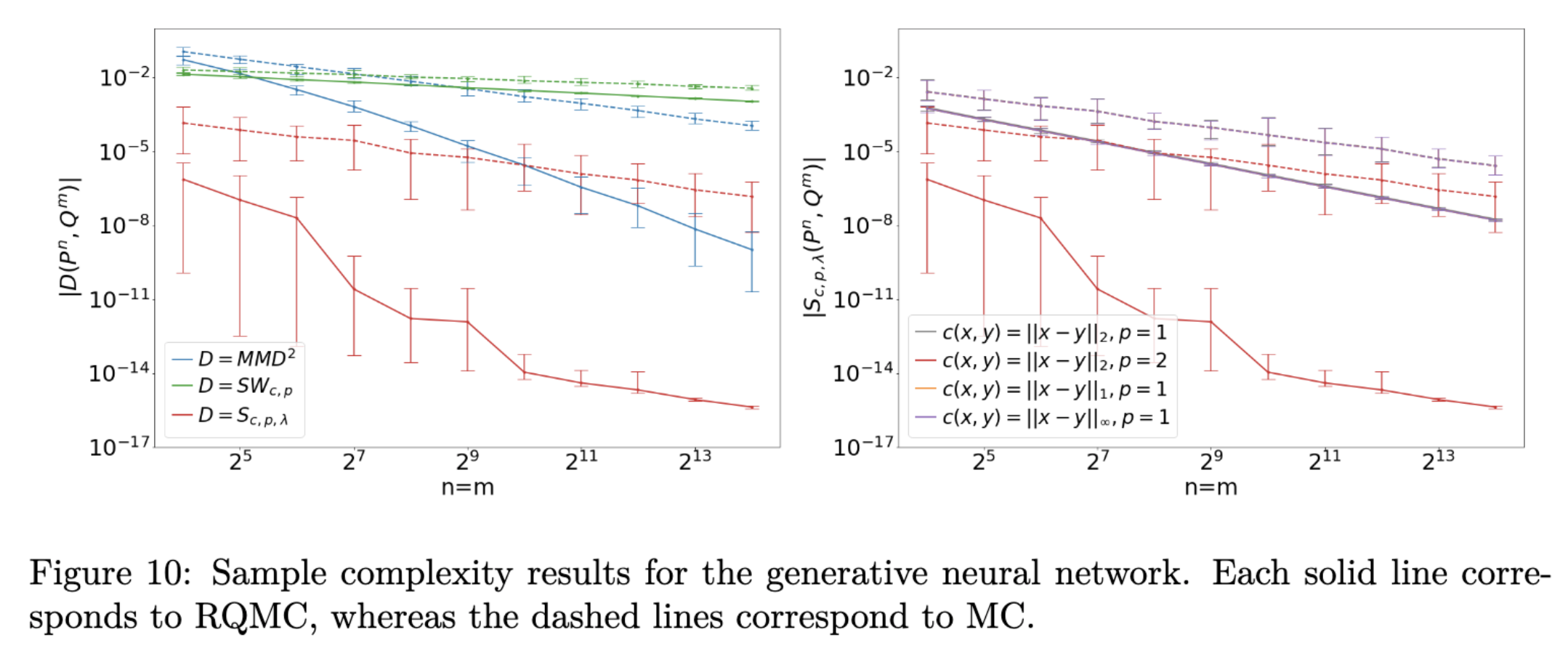
(PS: Randomized quasi-Monte Carlo (RQMC) is a randomized version of QMC where the evaluated points selected are now random.) (PPS: See here for a gentle introduction on Sinkhorn diverngece and its relationship with MMD.)
